Isoquant Curve: Meaning, Assumptions & Properties

This article try to explain the meaning of isoquant curve, assumptions and properties of isoquant. Also, it will describe about the marginal rate of technical substitution and economic region of production possibly in detail and obvious manner. In addition, I request you to go through the concept of production function, which will presumably ease your learning journey ahead.

• What is the meaning of isoquant?
• What is marginal rate of technical substitution?
• Why marginal rate of technical substitution diminishes?
• What are the types of isoquants?
• What is meant by elasticity of technical substitution between factors?
• Where is the economic region of production in isoquant?
• What are the general properties of isoquant?

Now assuming that you are familiar with concept of production function, let’s discuss the assumptions of isoquant curve. The main assumptions are:

1.  We use production function in modern form i.e. Q = f (K, L), with only two factor inputs capital and labor.
2. Technique of production remains constant.
3. Efficient use of all inputs in the production of output i.e. none inputs are idle or wasted. Exactly, production function indicates maximum quantities of output that can be produced by employing each and every combinations of factor inputs.

What is the meaning of isoquant?

Literally isoquant means equal quantity curve, it is also called as equal-product curve. We can define isoquant as the locus of various combination of factor inputs – capital and labor – that can produce same or constant level of output. In other words, isoquant represents all those combination of factor inputs that are capable of producing equal quantity of output. This way, a producer is indifferent with outputs represented by various points of isoquant curve.

Pictorial presentation of isoquants

Let’s present production function Q = f (K, L) in three-dimensional space to visualize what happens to output when more and more input combinations are used. By assumption of efficient use of factor inputs in production, the greater the employment of factor inputs, the greater the amount of output it will produce. That means to say, production function can produce Q1 level of output using K1 and L1 input combination, while it can produce Q2 level of output, the greater amount of output than Q1, using K2 and L2 input combination as represented along vertical output axis.

You can observe outlines of equal heights above KL plane corresponding to Q1 and Q2 level of outputs. These outlines are termed as isoelevation contours, and are as equal in height as corresponding Q1 and Q2 output levels. In fact, these contours are isoquants representing the same respective level of outputs, Q1 and Q2, that can be produced employing various respective input combinations lying in KL plane.

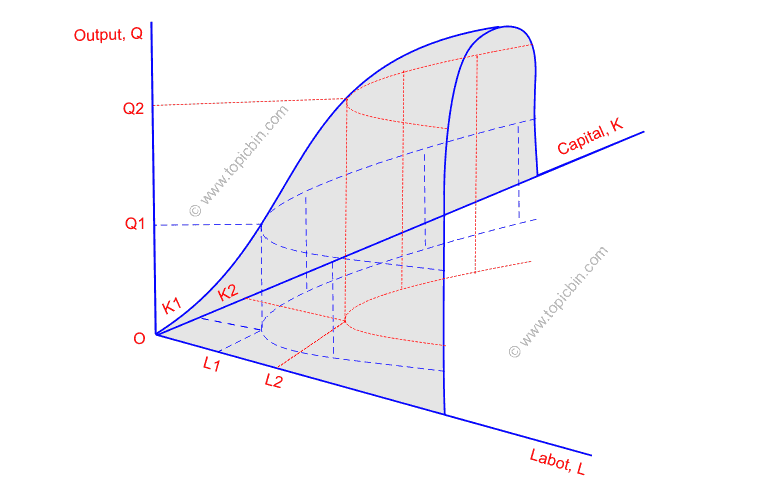
For the sake of simplicity, let us assume that these contours are projected to KL plane. And these contours – called isoquants – show various combinations of inputs that can produce particular level of outputs. Thus, each isoquant corresponds to a specific level of output and shows technologically efficient ways of producing that output. Hence, the simplified form of isoquants will be as follows:

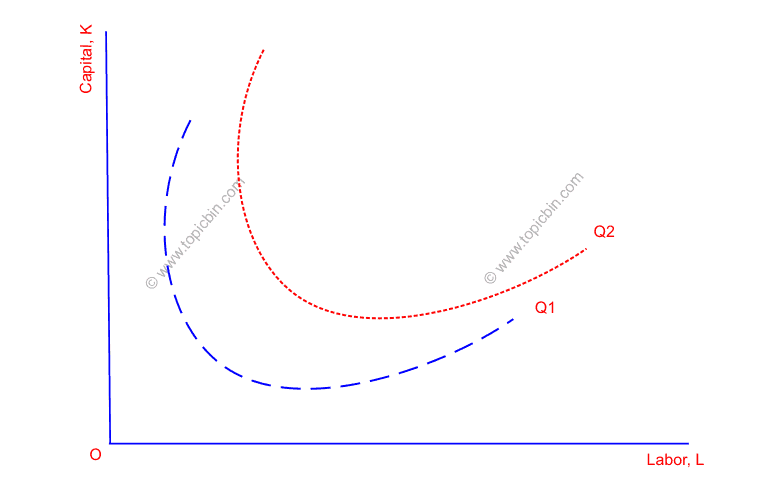
Also note, higher level of isoquant shows higher level of output i.e. Q2 is greater in amount than Q1. Thus, set of isoquants can depicts a production function.

What is marginal rate of technical substitution?

Marginal rate of technical substitution is a slope of isoquant which indicates the rate at which factor inputs can be substituted for so as to maintain the same level of output represented by isoquant. More specifically, marginal rate of technical substitution of labor for capital, MRTS_L,K, is the rate at which one unit of labor substitutes for units of capital holding constant the level of output. Likewise, we can define marginal rate of technical substitution of capital for labor, MRTS_K,L, is the rate at which one unit of capital substitutes for units of labor holding constant the level of output.

Graphically, we can present marginal rate of technical substitution, MRTS_L,K, as follows:

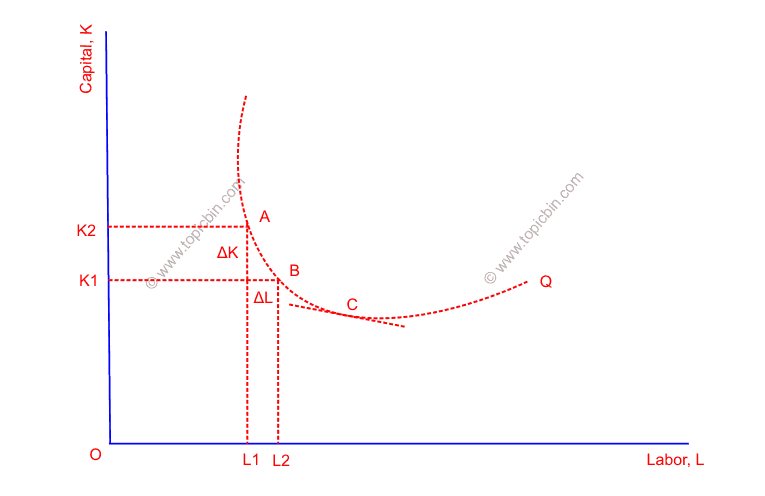
From this figure, we can observe that ΔK amount of capital has to be forgone in order to use additional ΔL amount of labor i.e. MRTS_L,K = ΔK/ΔL. This measurement is actually an arc marginal rate of technical substitution, which has measured MRTS_L,K in between points A and B. Nonetheless, point marginal rate of technical substitution of labor for capital at point C is given by slope of tangent at that point.

Mathematical presentation

Also following the definition of isoquant, or equal-product curve, we can write isoquant in mathematical form as

ΔKMP_K + ΔLMP_L = 0

or, ΔKMP_K = – ΔLMP_L  (subtracting by ΔL *MP_L on both sides)

Dividing on both sides by ΔL  and MP_K,

ΔK/ΔL = -MP_L / MP_K   ……………………. (I)

Also, using the definitions of marginal product of capital and marginal product of labor i.e. MP_K = ΔQ/ΔK and MP_L = ΔQ/ΔL, we can obtain the following result,

-MP_L / MP_K = -ΔK/ΔL    …………………….. (II)

Combining the results from (I) and (II), we get important relationship between marginal rate of technical substitution and marginal product of inputs as:

ΔK/ΔL = -MP_L / MP_K = -ΔK/ΔL

or, MRTS_L,K = -MP_L / MP_K = -ΔK/ΔL    …………………….. (III)

The result states that marginal rate of technical substitution equals and inversely relates to the ratio of marginal products, or productivity, of two factors.

Why marginal rate of technical substitution diminishes?

An important feature of marginal rate of technical substitution is that it diminishes along isoquant, which is called principle of diminishing marginal rate of technical substitution. And, this principle of diminishing marginal rate of technical substitution imply that fewer and fewer amount of capital is needed to use one more additional unit of labor.

The main reason behind diminishing marginal rate of technical substitution is that marginal product of capital increase as fewer capitals is used, and marginal product of labor decreases as more labor is used. Accordingly, lesser amount of capital is required to be replaced by greater amount of labor to keep constant level of output; and thus, marginal rate of technical substitution diminishes. In rigorous term, MRTS_L,K decreases because factor inputs are of imperfect substitutes.

However, marginal rate of technical substitution remains constant if factor inputs are perfect substitutes. In this case, isoquant curve will be negatively sloped straight line cutting K and L axes. Smaller the change in the MRTS_L,K, greater the degree of factor substitution. In opposite case, when factor inputs are not substitutes, then MRTS_L,K remains infinity or zero, and isoquants become kinked and parallel to K and L axes.

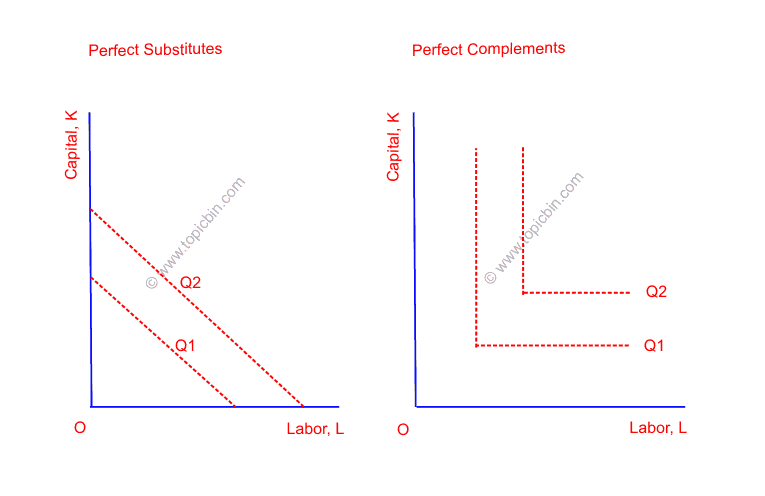
In case of perfect complement factors, vertical portion of isoquant shows zero marginal product of capital while horizontal portion shows zero marginal product of labor.

What are the possible types of isoquants?

Lets list out the possible forms of isoquats  under here:

• Linear isoquant- isoquant is linear when MRTS remains constant, which happens when factor inputs are perfect substitute. Look at the above picture of straight line isoquant.
• Input-output isoquant – isoquant is input-output when factors inputs are perfect complements to each other. It is also called Leontief isoquant, after Leontief , who invented input-output analysis. Look the L-shaped isoquant in above figure.
• Kinked isoquant – it is also called activity analysis isoquant or linear-programming isoquant because it is used in linear programming analysis.  It is kinked because of limited factor substitutability. And thus, production is efficient only at the kinked points of isoquant. This is actually discrete concept of production function, which engineer, manager, and production executive consider to be more realistic compared to continuous isoquant, which traditional theory mostly adopted for the sake of ease of exposition using mathematics and calculus.
• Smooth, convex isoquant – it is continuous isoquant with diminishing marginal rate of technical substitution and is convex to origin.

What is meant by elasticity of technical substitution between factors?

There is one serious defect in marginal rate of technical substitution as a measure of factor substitutability. It depends on measurement unit of factor inputs, therefore it cannot give true picture of factor substitutability. To circumvent this problem, another better measure of factor substitution comes to play – which is elasticity of technical substitution, or simply elasticity of substitution.

Elasticity of technical substitution is the ratio of percentage change in capital-labor ratio to percentage change in marginal rate of technical substitution. To say,

$$\text{Elasticity of substitution} (\alpha) = \frac {\text{Percentage change in K/L}}  {\text{Percentage change in MRTS}}$$

$$= \dfrac {\dfrac {\Delta K/L}{K/L}}  {\dfrac{\Delta MRTS}{MRTS}}$$

Elasticity of substitution between factors is a pure number free of unit of measurement, because both numerator and denominator are measured in same units that cancel out the units of measurement. Also note that when MRTS decreases K/L ratio also falls, and when MRTS increases K/L ratio also increases. This implies that elasticity of factor substitution is positive as least within the economic reason of production.

Where is the economic region of production in isoquant?

One important thing to consider here is that, not every input combinations are economically feasible to use in production. Therefore, a rational producer will abandon those unfeasible input combinations unless she is compensated for the use of those input combinations. These unfeasible input combinations are represented by positively sloped portion of isoquant.

Positively sloped isoqant means that firm must use both factor inputs if it chooses to use more of one inputs so as to keep the constant level of output. That means to say, using more of one inputs would actually cause output to fall unless more of other inputs were also used in production. The ultimate situation is marginal product of one factor inputs is negative along positively sloped isoquant.

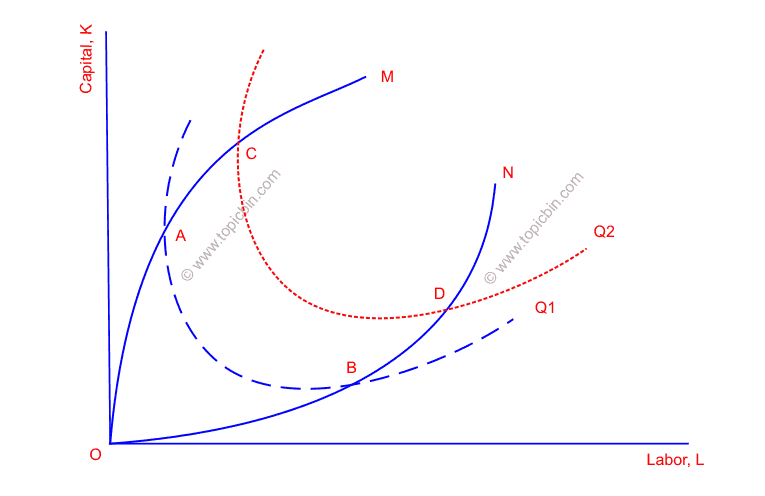
Economic region of production

In figure, marginal product of capital is zero at points A and C; and beyond those points (greater amount of capital) marginal product of capital is negative. Also note that more units of labor have been used in line with capitals along the positively sloped portion of isoquant to maintain the same level of output.

Similarly, marginal product of labor is zero at points B and D; and beyond those points (greater amount of labor) marginal product of labor is negative. Lines such as OAC and OBD are ridge lines, which connect points on isoquants having zero marginal products. The ridge lines bound area called economic region of production, in which marginal products of factor inputs are positive. Beyond the economic region of production, production is inefficient.

Factors having negative marginal product are called inferior factors, and we ruled out such inferior factors in production theory unless otherwise mentioned.

What are the general properties of isoquant?

Following are the general properties of isoquants:

 Isoquant slopes negatively

This is because of imperfect substitution between the factor inputs used in production. In addition, this negativity follows from the valid assumption of positive marginal product of factor inputs inside economic region of production.

Isoqunat never intersects to each others

If isoquants were to intersect to each other, it would imply different level of outputs (at point of intersection). Question arises, how could that be possible to produce different level of outputs with same input combination remaining unchanged the production technology? Which is against the fundamental assumption of isoquant.

Isoquant is convex to origin

This is because of the operation of diminishing marginal rate of technical substitution of factor inputs. Likewise, diminishing marginal rate of technical substitution will come in effect because of the imperfect factor substitution, which is again the result of operation of diminishing marginal returns of factors.  If isoquent were to concave, it would indicate increasing returns. However, diminishing returns is more true in real world.  Thus, we could assume diminishing marginal rate of technical substitution and accordingly isoquant convex to origin.

One problem with concave or straight line isoquants is that producer’s equilibrium results in corner solution. And, corner solution is a situation of employment of only one factor inputs in production. However, in reality, there are usages of more than one factor inputs in production. Hence, it is rational to have isoquant convex to origin.